Cosmic Staircase 3 - Triangles to the Stars

Triangles are wonderful things and ridiculously simple. All triangles have just six pieces of information:

The lengths of the three sides
The three angles between each pair of sides

The really cool thing is that with just two sides and one angle, or two angles and one side, you can work out all six values. If one of those values is the distance to a far away object we can measure it without moving from where we are.

Parallax is a particular form of triangulation and has been used to measure distance since ancient times. Thales of Miletus, a Greek mathematician and philosopher (624 BC to 546 BC) used triangulation to measure the height of a pyramid by comparing the length of its shadow with the length of his own shadow. Because he knew his height and that the angles of the triangle were the same as for the pyramid, it was a simple scaling calculation. He is also credited with working out how far away a ship was from the shore by observing from a cliff top of known height. There are also references to using triangulation in Egypt a thousand years before Thales. Then around 240 BC Eratosthenes, a Greek philosopher and mathematician, used triangulation to make the first calculation of the diameter of the earth and was only a couple of percent out. It has been used for surveying and map-making since the 16th century.

Parallax uses the right-angled triangle to measure distance, and you can try this for yourself.

Find a pencil and sit down opposite something vertical in your room, like the mullion of a window. Hold the pencil out at full stretch vertically in front of you, close one eye and line the pencil up with the mullion. Leave the pencil exactly where it is, then switch eyes. You have now visually separated your pencil from the mullion and created a right-angled triangle. It looks something like this:

To work out how far away the mullion is (D) without leaving your seat you only need two pieces of information:

The distance between your eyes (C)
Either of the two angles (A or B)

As this is a right angle triangle you can use the tangent of the angles to work out the value of D using either of these formulas:

D = C x tangent A D = C/Tangent B

As this is basic geometry, it is very precise and extremely simple. It is only the limitations of instruments (tape measures, theodolites, telescopes etc.) that introduce margins of error. We will deal with margins of error in another essay. You could do the same thing for the mullion of the window across the street, using the pencil again or your mullion as a reference point. You will notice that the separation between the two objects when you switch eyes is smaller. This is because the object whose distance you are trying to measure is further away and therefore the angle (B) is smaller. You could maybe still measure it, but with a larger margin of error. However the chimneystack a few streets away might produce too small an angle for your instrument to cope with. Of course you still know something important about that chimneystack. Namely, that it’s much further away than the things you have been able to measure. This is important because it tells you that the world is bigger than your ability to measure it.

So parallax is the technique for measuring distances beyond the reach of the investigator. Despite its disarming simplicity, the really brilliant thing about this technique is its ability to measure how far away really distant objects like stars are from earth. The only limitation is the instrument’s capacity for measuring the very small angles that such large distances produce (the angle B in the diagram below), and this is something that is constantly being improved. So what, in astronomical terms, is the equivalent of switching eyes? The answer is the annual orbit of the earth around the sun. It takes 6 months for the earth to travel half way around the sun and be opposite where it started relative to the star being measured.

Attempts to use parallax to measure the distance to stars were made from the 16th century onwards by such luminaries as Tyco Brahe (1546-1601), Galileo (1564-1642), Robert Hooke (1635-1703) and William Herschel (1738-1822). All of them were unsuccessful. The first time parallax was successfully used to determine the distance to a star was in 1838. Friedrich Bessel, Director of the Konigsburg Observatory achieved this using a device called a heliometer. He calculated the distance as 10.3 light years for the star 61 Cygni, which has since been determined more accurately as 11.4 ly. This is pretty good for a first attempt with relatively primitive equipment, being off by only 9.6%.

From these humble beginnings the use of parallax has evolved both fast and slow. Slow by the incremental improvements to instruments and techniques, and fast by the handful of step transitions that new technologies and ideas have allowed. The step transitions launched the technique into fresh surges into outer space that were, and still are, exhilarating and awe inspiring.

For 151 years from 1838 to 1989 all calculations of stellar distance were made using ground based telescopes. Even so the gradual improvement of instrument design meant that we were able to get as far out as about 130 light years, creating a sphere of stars 260 light years across and containing the distances (within ± 10%) of most of the 40,000 stars in that sphere. Even so this is only a tiny fraction of the stars in our own galaxy. The reason why 130 light years is the best we can achieve from earth-based telescopes is that light from the stars has to fight its way through the earth’s atmosphere, and this makes them appear to jiggle about as the molecules in the atmosphere jostle the photons. This is why 1989 and 1990 were step change years.

Into Orbit

Hipparcos

In 1989 the Hipparcos telescope was launched into orbit around the earth. It was the first space mission specifically designed for astrometry, the precise measurement of distances, positions, proper motions and magnitudes of stars. Over three and a half years it measured nearly 120,000 stars, 200 times more accurately than before. This gave us an unmatched 3-D description of the distances and motions of stars in our cosmic backyard. Hipparcos was decommissioned in 1993 after producing two catalogues of stars: The Hipparcos Catalogue for position and motion measurements and The Tycho Catalogue, for brightness. The European Space Agency website http://sci.esa.int/hipparcos has a huge amount of detailed information about the mission and is well worth a look. Hipparcos more than doubles the range of earth-based measurements using parallax. At ± 10% margin of error the radius of the sphere of stars is about 325 light years (650 diameter). This sphere contains over 500,000 stars. Hipparcos did more than just the astrometry, and the website lists some of these other achievements:

Helped to predict the impacts of Comet Shoemaker-Levy 9 on Jupiter
Identified stars that will pass close to the Sun
Established the distances of stars possessing planets
Cut the distance of the Pleiades cluster, forcing a rethink about star theories
Discovered that the Milky Way is changing shape
Identified a group of stars that invaded our Galaxy when it was young
Altered the cosmic distance scale, making the Universe bigger and younger
Confirmed Einstein's prediction of the effect of gravity on starlight.

Hubble Space Telescope (HST)

A year after Hipparcos the Hubble telescope was launched. Hubble achieved distance measurements of around 1000 light years until 2013. In that year astronomers at NASA started using a technique called Spatial Scanning. This involves taking multiple measurements 6 months apart, a technique that allows “noise” to be much reduced. This has the effect of eliminating errors to produce accuracy in measuring parallax angle that is more than 10 times better than previously achieved. Hubble is now measuring distances to stars up to 10,000 light years away. This means we are measuring the distance of stars across a sphere of 20,000 light years. They are concentrating their efforts on a type of star called a Cepheid Variable, which plays an important part in validating the accuracy of other techniques in the distance staircase: More of that later.

Gaia

On 19 December 2013 the Gaia telescope was launched from French Guyana. Gaia is a completely new and stunningly accurate design of telescope. It will measure, using parallax, the precise distance and motion of around 1 billion stars. On the 8 January 2014 Gaia reached its final position at L2, the second Lagrange point beyond the moons orbit and a further million miles from the sun than the earth. The five Legrange points are locations in space where the combined gravitational effect of the earth and sun cancel each other and allow any object at that location to remain in place more easily with respect to both. For more info go to http://map.gsfc.nasa.gov/mission/observatory_l2.html or search Legrange Points.

Repeatedly scanning the sky, Gaia will observe each of its billion stars an average of 70 times each over five years. In addition to positions and motions, Gaia will also measure key physical properties of each star, including its brightness, temperature and chemical composition.

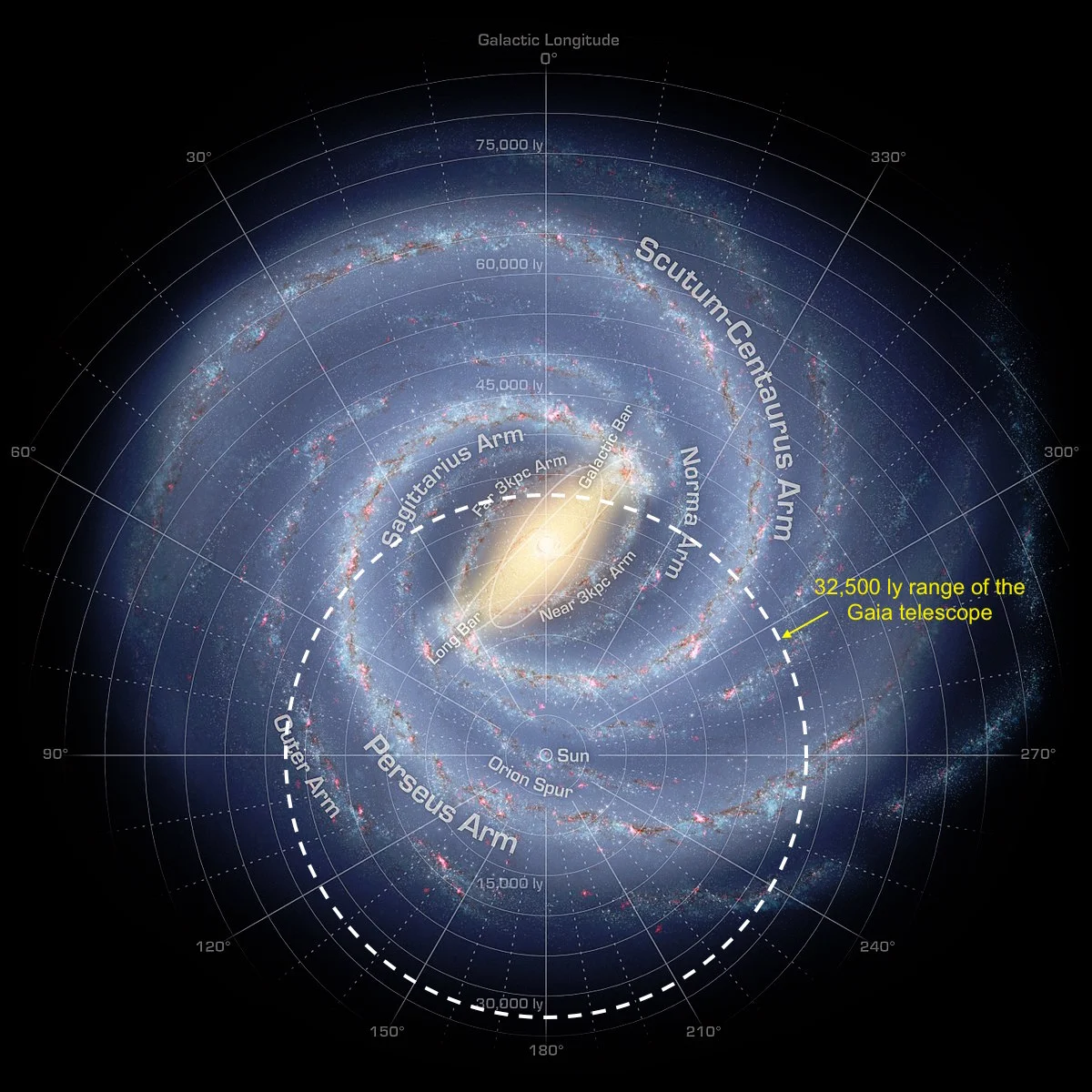
About 20 million stars will be measured with a distance precision of ±1% and about 200 million will be measured to better than ±10%. Distances accurate to 10% will be achieved as far away as the Galactic Centre, 32,500 light-years away. With that range we will be looking back in time 32,500 years with unprecedented precision, and we will have mapped in detail most of the stars across 65,000 light year sphere of space. As well as this most exciting of jobs Gaia also watches the rest of the Universe. On 30 August 2014 it spotted a supernova in a galaxy 500 million light years away. As well as working out the proper motion of stars it will also track the motions of the Large and Small Magellanic Clouds to within 2 or 3 km per second. You can find out more about this and follow the activities of the telescope on its dedicated website.

The image above is an artists rendition of our Milky Way showing the various spiral arms. We now have enough data to map this quite accurately and you can see that the sun is in a relatively minor spur, the Orion Spur of the Sagittarius Arm.

The aftermath of Supernova 1987A showing the ring energised by the supernova ejecta. Source http://www.eso.org/public/images/eso1401a/

Supernova SN1987A

You might think that we have reached the limits of triangulation as a method for calculating distance. You would be wrong. On February 23, 1987 a star in the Large Magellanic Cloud (LMC) went supernova as seen from Earth. About a year later gases around the star were ionised by the ultraviolet flash from the explosion. This, plus the speed of light, gave us the diameter of the ring and then triangulation gave us the distance to the supernova with an error of less than 5%. The LMC is a dwarf galaxy lying just outside our own Milky Way. It’s a sort of Milky Way groupie. It turns out that SN1987A is about 168,000 light years away, and this is additionally useful because it validates the other methods used to calculate the distance of the LMC itself, as we will see on the chart at the end.

You can see from the local group projection below that the LMC is one of a number of dwarf galaxies that are effectively satellites to the Milky Way. The only other large galaxy nearby is Andromeda, which is 2.5 million light years away. It is included in the local group because the gravitational attraction between the two galaxies overcomes the overall expansion of the universe, and they are moving towards each other at 300km per second or 1,100,000km per hour. They will collide in about 4 billion years time, although ‘merge’ is probably a much better term. It is highly unlikely that we will be around to worry about it.

Our local galactic group. Source - Wikimedia, Andrew Z. Colvin

Triangulation, and parallax in particular, is my favourite technique for measuring distance. Forget the complexity of the technologies required to measure the angles; these are just the tools for the job. Triangulation is beautiful in its simplicity and unquestionably honest in what it tells us. That we can use the humble triangle to take us beyond the confines of our own galaxy to one of our closest stellar conurbations is beyond magic or fantasy or religeon. It is, in my humble opinion, one of the many spiritually awesome things in the continuously growing body of our knowledge, not least because we have managed to nurture our curiosity to the point of being able to understand it so well. The Local Galactic Group image above is beautiful and part of its beauty lies in how we can use it to understand our place in the universe.

Parallax is the first step in the cosmic staircase, starting with our nearest stellar neighbour, Proxima Centauri, then the first attempt in 1838 to use parallax on 61 Cygni, all the way via increasingly powerful space telescopes to supernova SN1987A.

The chart below is my own. It shows the five techniques that form the backbone of this series of essays.