Cosmic Staircase 2 - The Prequel — How Knowledge Works

We’ve always measured distances to things, long before we ever reached out to the stars. From setting out where the foundations of a building will go, to drawing an accurate coastline or working out the height of a mountain, we have found ingenious ways to measure things. The increase in the distances we measured tended to be gradual ones with the occasional giant leap, usually because the next thing we could measure was hugely further away than anything we’d managed so far. These giant leaps always required the invention of new techniques and equipment. So the insatiable desire to find out how far away things are has nurtured our inventiveness.

The furthest distance measured on earth was the circumference of the earth at around 40,000 kilometres. To go further than that we needed to tackle the moon, nearly 10 times further. Then we picked up the distances to our other solar system companions incrementally until we got to Pluto, which is 7.5 billion kilometres or about 5.5 light hours away. The next giant leap is what begins our cosmic staircase and is the subject of further articles. The nearest star, Alpha Centauri, is 7000 times further away than Pluto. In this article I’m only going to go as far as Pluto, so lets start with the Romans.

Our capacity for observing and measuring the world without any enhancements to our natural senses is pretty good, but generally limited to the human scale of things. Until fairly recently even to measure the dimensions of a room required our physical presence at both ends, at the very least to attach the end of a measuring tape to one of them.

The longest distances measured in this way historically are by pacing. The usual method is to count your paces for a given distance. The romans used the double pace of its soldiers, taken to be about 5 feet, with 1000 of these being a mile. In this way the potential distances that can be measured is only limited by stamina and the availability of land to walk on, and of course not losing track of the counting.

‘Sorry lads, got distracted, we’ll have to go back to Londinium and start again.’

Pacing, and also dead reckoning at sea, is inherently inaccurate, but there were no viable alternatives back then. Despite this we have not given up on pacing in the 21 century. Wearable devises can now count your paces, primarily for health reasons. This illustrates an interesting relationship with precision. How much accuracy is needed for a given task? For exercise the number of paces is more important that the distance travelled. Even when we wanted as much precision as we could get, we knew it could never be perfect. Every device ever made to measure something was manufactured to a tolerance, and utilised with a built in margin of error. A 5 metre steel measuring tape for example is made to a tolerance of ± 1.3mm, and in use can vary by another couple of millimetres depending on the ambient temperature. I will explore precision in another essay.

Being able to work out the distance between two points without having to move from one of those points represents, quite literally, a big step up in scale, with each new method taking us further out. Lets start with triangulation.

Triangulation

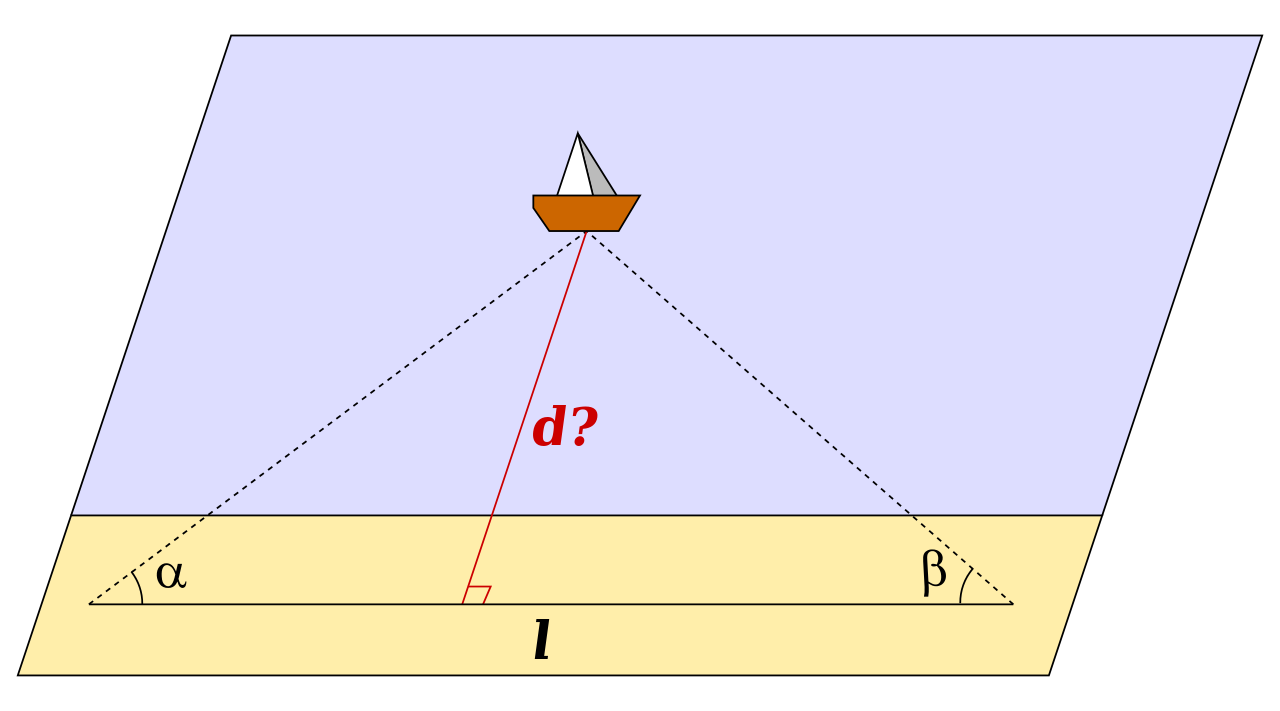
Triangulation is ridiculously basic, but very powerful. It was Pythagoras (570 - 495 BC) who codified the relationship between the three sides of a right-angled triangle and ever since then people have used its simple formulas to set out buildings and survey land. The methods are not confined to right angle triangles. If you know either one angle and two sides, or two angles and one side of a triangle, you can work out all three angles and sides.

Left is an example of how this can be used. A ship is observed from two different locations on shore. The distance between the two locations is known (l), and the angles (α and β) are measured from each location. From just this information we can work out how far away the ship is (d).

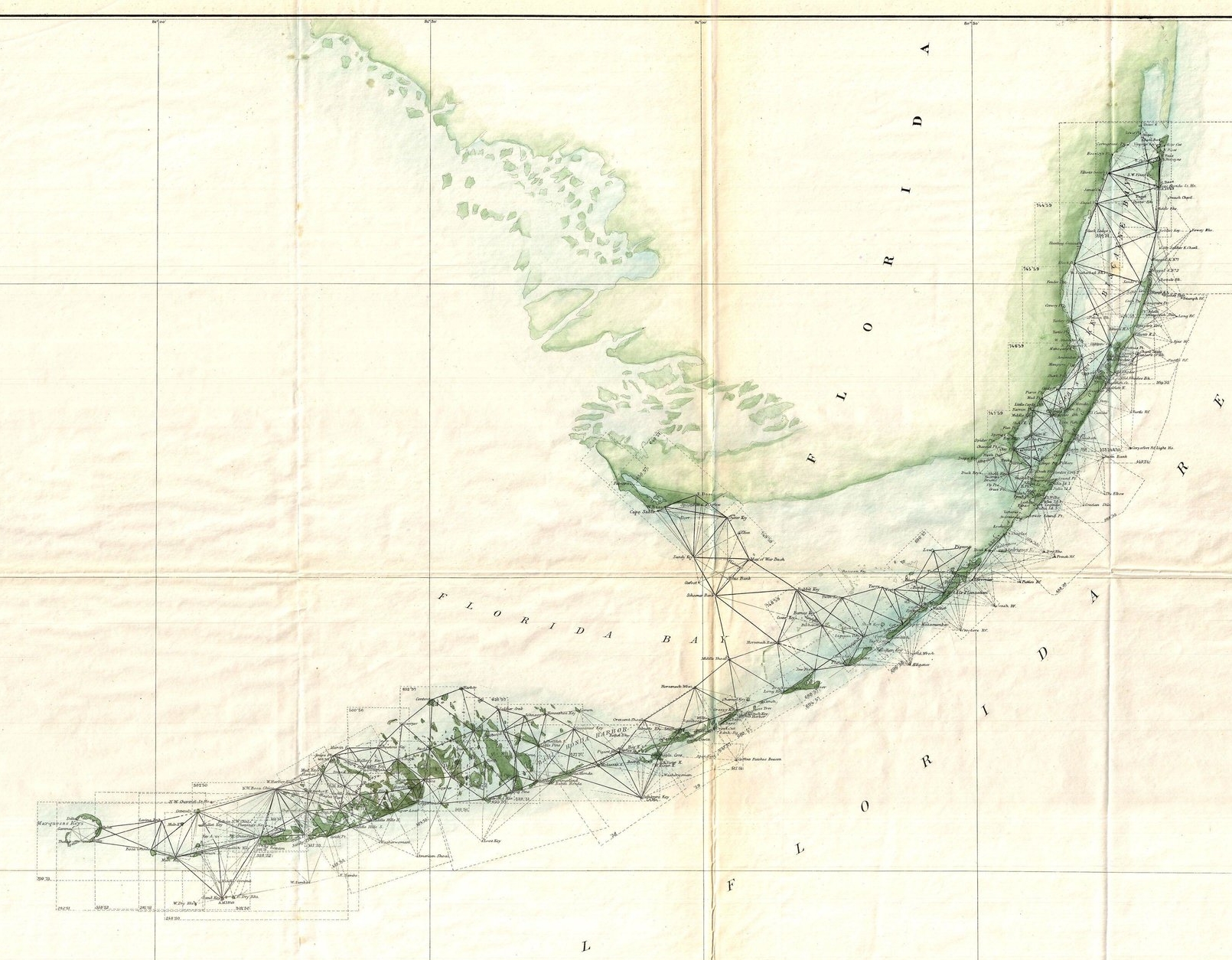
Arabic scholars first introduced triangulation for land surveying around 1000 AD, and by the 16th century cartographers were routinely using it for detailed mapping. The image to the left is a US coastal survey of the Florida Keys and south coast published in 1859. The method, linking points on the land with multiple triangles is called a triangulation network.

Triangulation network of the Florida Keys and south coast (1859). Image from Wikimedia Commons, Geographicus Rare Antique Maps

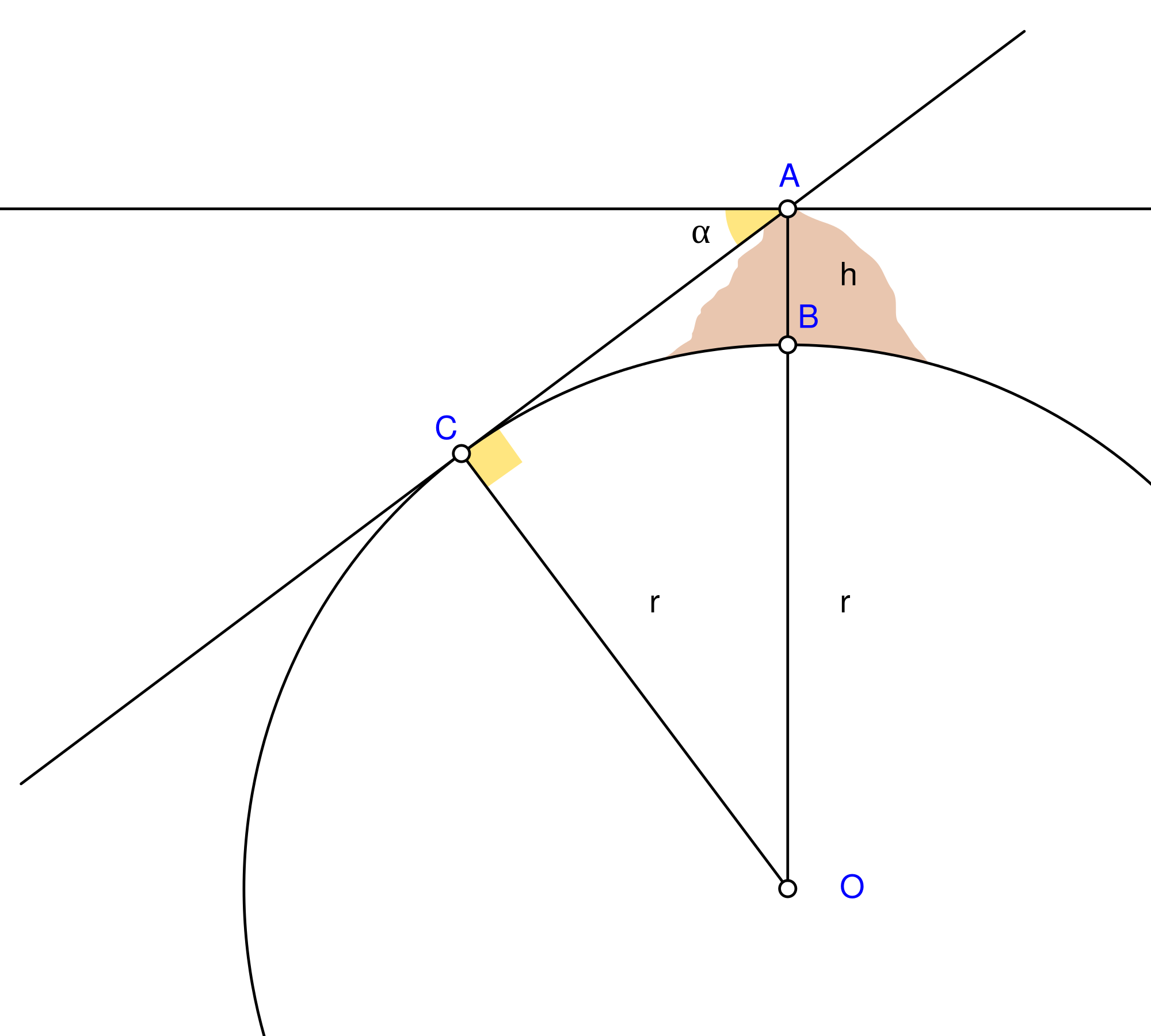
Biruni (973 - 1048) used triangulation to work out the radius of Earth. Source - Wikimedia, Nevit Dilmen

Eratosthenes first calculated the circumference of the earth around 240 BC. A description of this can be found in the article ‘The Journey”.

Here I will describe a method that calculates the radius of the earth first. Once the radius is known the circumference can be worked out.

Abū Rayḥān Muḥammad ibn Aḥmad Al-Bīrūnī, a Persian scholar from the 11th century, used the known height of a mountain to create a right angle triangle, from which the radius could be calculated. He got within 17 kilometres of the correct measurement.

Hipparchus method for calculating the distance to the moon. Source - Wikimedia, Dantheox

The first reasonably accurate calculation of the distance to the moon was made by Hipparchus (190 - 120 BC). He used a solar eclipse in 129 BC to triangulate relative to the sun from two different locations on Earth simultaneously, The Hellespont and Alexandria. The Hellespont was a total eclipse and Alexandria was partial. In his first attempt he overestimated by about 25%. His second attempt was a bit better at about +10%. Three centuries later Ptolemy (100 - 170 AD) did even better with the same method, getting within 2%.

Bouncing signals

Laser

If you can direct a beam at a distant object and bounce it back to you, and you know the speed of the particles in the beam, you can work out how far away the object is. This principle has many uses, from surveying the dimensions of buildings with small laser devices, to radar and bouncing signals off layers in the earth’s crust to determine depth of different zones. In 1962 the Massachusetts Institute of Technology (MIT) conducted experiments bouncing lasers off the surface of the moon. The Crimean Astrophysical Observatory repeated this a few months later with similar results. In 1969 the Apollo 11 mission left an array of retro-reflectors on the surface, with more arrays placed by Apollo 14 and 15. The combination of these arrays and improvements in equipment has led to spectacular levels of accuracy. One of the findings is that the moon is receding from the earth by 3.8 cm per year. The overall distance varies because of the elliptical orbit, but averages around 384,467 kilometres. This is an extract from the book ‘Laser – Surface Interactions’ by the Rashid A. Ganeev of the Uzbekistan Academy of Sciences.

'At the Moon's surface, the beam is about 6.5 kilometres wide and scientists liken the task of aiming the beam to using a rifle to hit a moving dime 3 kilometres away. The reflected light is too weak to be seen with the human eye, and out of 10,000,000,000,000,000 photons aimed at the reflector, only one will be received back on Earth every few seconds, even under good conditions. They can be identified as originating from the laser because the laser is highly monochromatic. This is one of the most precise distance measurements ever made, and is equivalent in accuracy to determining the distance between Los Angeles and New York to 0.25 mm.'

At 4000 kilometres between the two cities this is ± one 300 millionth of a percent.

Artist depiction of the New Horizons spacecraft near Pluto and its moon, Charon. Source Wikimedia, NASA

Radio

Since we sent probes into space it has been possible to measure distance by sending a radio signal to the probe, which responds by sending the same signal back. This extract is from the website dedicated to the New Horizons spacecraft, launched in 2006 to flyby Pluto and send back images:

http://pluto.jhuapl.edu/Mission/Spacecraft/Systems-and-Components.php

New Horizons is the first mission to use onboard regenerative ranging to track the distance between the spacecraft and Earth. When a spacecraft is far from home, the ranging tone sent from the ground to measure distance is weak (or “noisy”) by the time it reaches the spacecraft’s communications system. In normal ranging, the spacecraft simply amplifies and sends the noisy tone back to Earth, which adds errors to the range measurement. In regenerative ranging, the spacecraft’s advanced electronics track and “regenerate” the tone without the noise. The ground station on Earth receives a much clearer signal – giving navigators and operators a more accurate lock on the spacecraft’s distance, and improving their ability to guide New Horizons through the solar system.

Theoretically we could do this for any distance, provided the technology delivered a readable return signal. So far Pluto, which has a very eccentric orbit, is the best we’ve managed, and varies between 4 and 7 light hours away from earth. It doesn’t seem unreasonable to suppose that when we eventually range beyond the solar system, either as people or machines, that we will be able to send and receive signals. Undoubtedly this will be accompanied by the calculation of distance. However far we range outward with this method, we are very unlikely to surpass the range of the first major distance technique, and the first proper step in the cosmic staircase: As we have seen here triangulation is the only method used within the solar system that is also capable of measuring the distances to stars. In fact in one particular instance it gave us the distance to the Large Magellanic Cloud, which is 168,000 light years away. I will tackle this in the next article.